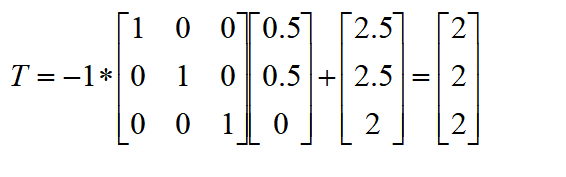機械社區
標題: 已知面角,如何求歐拉角,機器人坐標變換怎么求? [打印本頁]
作者: 水水5 時間: 2025-7-26 18:44
標題: 已知面角,如何求歐拉角,機器人坐標變換怎么求?
問題的來源是這樣的:5 s3 U2 R, u, p$ y
( S5 g8 D! M7 O$ [$ r e! ]
有一個項目,機器人末端的手爪,因為種種情況,設計了一個傾斜的吸盤。需要在3D視覺的引導下,去吸取一個傾斜的物體。
/ a. @- v$ Y P; Y, E5 ]7 f' n機器人編程工程師嫌手工做工具坐標系比較費時費力,問我能否通過三維軟件,求得坐標變換的數值,直接填入機器人系統中的工具坐標系的標定參數中。
0 ^, k# g# f( T$ g. V我感覺應該挺簡單的呀,于是就在三維模型中(我是用solidworks進行的建模)建立了兩個坐標系,一個是安裝法蘭的坐標系,一個是吸盤面的坐標系。
+ _) y: c( N( f然后測量了兩個坐標系的位移,和角度,然后給了機器人編程工程師
; _* U" }9 K* g1 T
+ @2 a# R* u, W6 T結果發現不對(測試方法:走軸坐標ABC,并不能繞坐標系原點旋轉,證明坐標系不對)
# b3 W( x$ K. `* {+ a) O" g" m! {4 y S% o; R
兩個坐標系的位移很好測量。兩個坐標系的角度,我是這樣測量的,我的solidworks版本低,沒法直接給出數,于是我建了三個面,例如要測量Z軸之間的角度,我就測量了兩個XY平面的角度。
& R }+ H; \8 _- i) E/ T$ _
, H" {9 a4 w5 L5 U于是我將這個問題抽象出來了,花了大量的時間研究面角,歐拉角,也沒研究明白。發現這個歐拉角,這個三個軸的旋轉順序還有要求,有ZYZ,有XYZ,可能各個品牌的機器人還不一樣。
+ L! {( r0 Z/ g. W8 O9 c+ { Z+ b
0 W3 X% {# t- A$ k0 j7 b我抽象了模型,問了AI,竟然說我這樣的坐標系不存在?6 G& c; L" y" d4 N
4 y# I% r: ]" S: ]5 I1 Q下面是我抽象出來的數學模型:兩個坐標系的三個面之間的角度都是30度,坐標系原點重合,求坐標變換歐拉角。# u7 e" u" X D c# p( Y
3 l& M3 z$ I ]7 ^3 F
有沒有高手給解答一下。& o, k$ f( d8 t# q4 s7 D" N
( W& s3 W6 r* D0 G以下截圖是這個兩個坐標系的空間位置
9 G1 U* |' |1 L! B[attach]577212[/attach]
3 h4 }2 ~+ V" _9 D( B) F8 U( z[attach]577213[/attach]
: N8 a2 Q! ^ _2 H& j[attach]577214[/attach]
" e; W7 s# x2 v9 [6 M3 s, ` c[attach]577215[/attach]& [3 K! \! i5 W! k p# ^- d6 Q
作者: 學者11 時間: 2025-7-26 19:12
機械手變換坐標系要是這么容易,那何來機械臂動力學和D-H建模法呢。
9 R9 k. |& C: ~( {+ i( T2 Z# n0 d" u先了解點基本常識吧,https://zhuanlan.zhihu.com/p/692369673
作者: ckc521 時間: 2025-7-26 20:52
樓上正解;五軸機床轉換你懂不?你可以把機器人看成一個五軸機床,用DH法建模來求解旋轉角度,從機械手末端到基座,或者從基座到機械手末端,都可以推導出來。" ~# x$ [+ Y" [0 v6 F/ \" Y" r
作者: ckc521 時間: 2025-7-26 20:53
還有別問國內的AI,國內的AI,連歐拉角動態旋轉和靜態旋轉的等效性都不會給你正確的推導出來。
* X# y6 |* V+ k" E" Z" t! r
作者: 夢里啥都有 時間: 2025-7-26 21:40
不懂,但是AI只能夠搜資料,有時候給不了出處的還不能夠信.8 J8 ~% k" P7 e+ x
何況復雜的建模肯定少不了計算的優化.$ g/ Y& o" N& u6 s4 x; {7 C
矩陣肯定少不了需要高效的算法.' ~+ }3 O5 s# I9 ?5 f4 q0 h1 u
我只會簡單的x^x+y^2=1
, w" }8 g5 f5 h8 Ox=cos(theta),y=sin(thea)
) D% b: s. o% ^5 q- Y! m0 g4 E這些東西肯定少不了各種知識.! I m/ E8 a) M) k& N1 {
與其糾結,不如先把路走遠,再走深.* a* V4 Q9 @ X3 k' U/ o3 N Q
作者: cc851 時間: 2025-7-27 07:22
機械工程師解決不了現場調試的痛,模型上永遠都是理論的,何況這么多零件組裝在一起的累積誤差,對于相機和機械手的計算補償來說都是災難。最近幾年一直做復合機器人的項目,一直頭痛精度問題,都和這些有關系。
作者: 冷月梧桐 時間: 2025-7-27 14:23
直接把機械手模型和治具導入SW/各類機械手軟件,模擬點位,然后出各個軸的角度數據就好了
作者: DaedraMech 時間: 2025-7-28 11:56
本帖最后由 DaedraMech 于 2025-7-28 12:32 編輯 ) P# M: }# U+ p- C* z
) l m: F( q. S不知道我有沒有正確理解樓主的意思,我先談談自己對坐標變換的理解:) b5 Q: {) \' w; G+ `+ c- w9 T
坐標變換矩陣既是變換參數(轉角、位移),又是變換后坐標系的基底在原坐標系上的坐標組合。( z8 B) S# |0 q* r2 t6 [/ q8 n
* |1 i) n" i2 V9 n& P+ r3 _
樓主在SW中使用的方法是控制三個正交平面和原平面各成30°,我個人更喜歡直接建立坐標系,由于x軸是YZ面法向量/y軸是XZ面法向量/z軸是XY面法向量,所以我約束3個新坐標軸和原坐標軸各成30°達到效果和樓主應該是一樣的。三個基底([ix iy iz],[jx jy jz],[kx ky kz])有9個未知坐標值,有【3個基底長度為1】、【新基底和原坐標軸各成30°】、【基底之間互成90°】這9個約束一定能在SW中畫出3個代表基底的線段,由此即可建立新坐標系,測量線段端點的坐標值即可獲得變換矩陣。
Z" N8 _* M q+ ][attach]577235[/attach]5 o7 n! B7 g0 @; D
[attach]577228[/attach]2 d2 [$ v/ _% u$ [: C% C( r+ a
我們來測試一下,我們假設工具坐標系上有一點[0.5 0.6 0.7]',我們想知道該點在法蘭坐標系上的坐標值,那就可以用變換矩陣左乘這個向量:
# X8 h: s0 U# q. C[attach]577230[/attach]3 o4 U. F+ v0 L, R( ~
把獲得向量的坐標值輸入SW,測量下它在工具坐標系下的坐標,果然還是[0.5 0.6 0.7]',變換矩陣是正確的:! x' v# P3 \, W* u/ K3 ` Y$ S& y N
[attach]577234[/attach]* P* U, U8 v, M1 c6 a" J
[attach]577233[/attach]
, T. ]' O6 a3 c4 P _! ?; @3 Y如果坐標系還有位移,可以使用齊次變換矩陣進行變換:
( X; y$ U! o) }[attach]577228[/attach][attach]577231[/attach]! W! e5 h( i5 B/ K
上面的演示中,樓主可以看到,矩陣里的坐標值就是特定角度的正弦/余弦值,所以歐拉角可以從這些角度中拆解出來,也就是總變換矩陣可以拆解成一系列單軸角度變換矩陣連續左乘,由此可以表示出坐標系繞各軸旋轉的角度和先后順序,這也就是樓主說的“面角轉換為歐拉角”,過程較為麻煩,我個人不推薦這種方式。
1 u! L, ^1 t' x# A% \9 [0 z3 z! B) A5 S9 h: B1 t' f. @* }+ I% H
( X8 i7 p' b/ g/ E _& m* X1 h, X' h" |' U6 P
作者: DaedraMech 時間: 2025-7-28 14:23
本帖最后由 DaedraMech 于 2025-7-28 15:41 編輯 ) o+ ], N) I0 `/ @0 e
DaedraMech 發表于 2025-7-28 11:56, ~! M* H/ \3 H1 Z5 b0 a
不知道我有沒有正確理解樓主的意思,我先談談自己對坐標變換的理解:% G% K% y" F% `6 W9 G/ Y' K
坐標變換矩陣既是變換參數(轉角、位 ...
* B3 K% {7 W$ g一般對算法這邊來說最直接的就是拿到變換矩陣了,不知道為什么還要舍近求遠獲得歐拉角,不過樓主需要的話可以按照下圖解方程,獲得各軸轉角和順序。另外,方程是多解的,比如【先繞z軸逆時針旋轉17.927°,再繞y軸順時針旋轉24.465°,再繞x軸順時針旋轉17.927°】就是其中一個解:
( s% S s, d) c1 f
6 C. i0 D7 Z; n3 ~: _[attach]577238[/attach]
) }0 q+ J/ y" g, b8 J. Y2 B6 Y9 m5 p, l& s d. M, I8 C
作者: sen1234 時間: 2025-7-28 18:11
線性代數嗎,都忘得差不多了
作者: 水水5 時間: 2025-7-29 19:18
; Q9 b- E1 v) G- P$ |: _
感謝層主,膜拜( `+ T+ h) c( s) N4 r0 x8 f6 A" `
+ B- m* c- R6 {! m- v5 q
我一定把它付諸實踐- u: @$ E: j* u- N4 ~
( ` J' \8 c" f2 j! X7 A我又搜索了一些其他的方法,再次請樓主給于指導。一些方法貼入后面的回復。9 N, D' A( y7 c. \
作者: 水水5 時間: 2025-7-29 19:20
" N) q4 z2 S8 P3 M: W
+ a L. q; e4 e# X$ w- ?方法一 本文轉載自簡書,作者是梁間。表示感謝: J# d5 Y" E& g2 e, P! o/ `$ S
數學模型已知兩個坐標系在各方向上尺度縮放比例一致,兩個坐標系的轉換關系可以用7個參數來表示,3個旋轉參數,3個平移參數,1個比例參數。已知三點在A、B兩個坐標系中的坐標,那么這7個參數可以唯一確定。1 R. ]4 I! i7 J& Z' i! S& b
坐標轉換的數學模型為:
- J' q/ F, i$ T2 R& h3 R%20...(1))
8 g2 C0 Y4 _6 p其中,λ是比例參數,R是旋轉矩陣,Δ是平移向量,A、B分別是兩個坐標系中的坐標。/ i" \, | F0 N$ W# i. n! P9 S
比例參數λ最容易計算" u- Q/ k5 D- ?8 F

, A1 `1 a- M, l+ A其中 為
為 兩點在A坐標系中的距離。( K7 L5 p W5 w% z* n
兩點在A坐標系中的距離。( K7 L5 p W5 w% z* n
旋轉矩陣R是一個3x3的正交矩陣,有3個自由度。可利用反對稱矩陣S來構造旋轉矩陣R:
' }) w6 K R. R3 L* h
0 C# w6 f, x7 B: m- D$ a, H1 N那么% |7 v5 m9 M/ l
) * I; h+ v& t6 Y0 b' h N+ N: K
* I; h+ v& t6 Y0 b' h N+ N: K
其中I是單位矩陣,這里R只有a、b、c三個變量,解出a、b、c即可確定旋轉矩陣R。, V5 U% Q9 x: ~8 L8 x6 ` | E
把 兩點帶入(1)式并相減消去ΔX、ΔY、ΔZ8 V [, H. V; s/ h! u
兩點帶入(1)式并相減消去ΔX、ΔY、ΔZ8 V [, H. V; s/ h! u
)
1 O# @6 f! z! V% s' y這里 為
為 點在A坐標系X軸向坐標值,為已知量。我們簡化一下寫法設定:
點在A坐標系X軸向坐標值,為已知量。我們簡化一下寫法設定:
7 c) f% i- Z6 w ) y# K8 w0 E( j/ p2 m! ^
) y# K8 w0 E( j/ p2 m! ^
這樣(3)式可寫為' O! P5 j0 J/ B9 T! n% [' m
) - E( f9 `, A. Z' K& y" l- c: [4 ]
- E( f9 `, A. Z' K& y" l- c: [4 ]
把(2)式帶入(4), q. x# A2 Y7 \ U2 W4 f7 c
%5Cbegin%7Bbmatrix%7D%20X_%7BA12%7D%5C%5C%20Y_%7BA12%7D%20%5C%5C%20Z_%7BA12%7D%20%5Cend%7Bbmatrix%7D%20%3D%20%CE%BB(I%2BS)%5Cbegin%7Bbmatrix%7D%20X_%7BB12%7D%5C%5C%20Y_%7BB12%7D%20%5C%5C%20Z_%7BB12%7D%20%5Cend%7Bbmatrix%7D)
4 ]4 S* P8 Z* W B. S0 k& r' ]帶入S
. D H3 y! H% q% ]/ |5 T0 H. T9 x
. E+ m" I% i% f% j$ z/ T5 I展開* A9 y5 L) ^) [9 i
 ' L" g& j! m0 C7 k
' L" g& j! m0 C7 k
整理可得/ W* ? O; U) [! E! N
-b%CE%BB(Z_%7BB12%7D%2BbZ_%7BA12%7D)%5C%5C%20c(%CE%BBX_%7BB12%7D%2BX_%7BA12%7D)-a(%CE%BBZ_%7BB12%7D%20%2BZ_%7BA12%7D%20)%5C%5C%20b(%CE%BBX_%7BB12%7D%2BX_%7BA12%7D)%2Ba(%CE%BBY_%7BB12%7D%2BY_%7BA12%7D%20)%5Cend%7Bbmatrix%7D...(5))
! I' L0 _6 [, H9 a: C1 m; b(5)式只有兩個獨立方程,解不出a、b、c三個未知量。帶入 點得到和(5)式類似的方程組,兩個方程組聯立,取3個獨立方程
點得到和(5)式類似的方程組,兩個方程組聯立,取3個獨立方程
$ i# C+ \& A5 e/ W2 U, y( g%20-c(%CE%BBY_%7BB12%7D%2BY_%7BA12%7D)%20%5C%5C%20-a(%CE%BBZ_%7BB12%7D%20%2BZ_%7BA12%7D%20)%2Bc(%CE%BBX_%7BB12%7D%2BX_%7BA12%7D)%5C%5C%20a(%CE%BBY_%7BB13%7D%2BY_%7BA13%7D%20)%2Bb(%CE%BBX_%7BB13%20%7D%2BX_%7BA13%7D)%5Cend%7Bbmatrix%7D) " C+ t% }0 f, ^1 o3 E% A
" C+ t% }0 f, ^1 o3 E% A
%20%26-c(%CE%BBY_%7BB12%7D%2BY_%7BA12%7D)%20%5C%5C%20-a(%CE%BBZ_%7BB12%7D%20%2BZ_%7BA12%7D%20)%26%200%20%26%20c(%CE%BBX_%7BB12%7D%2BX_%7BA12%7D)%5C%5C%20a(%CE%BBY_%7BB13%7D%2BY_%7BA13%7D%20)%26b(%CE%BBX_%7BB13%20%7D%2BX_%7BA13%7D)%260%5Cend%7Bbmatrix%7D%20%5Cbegin%7Bbmatrix%7D%20a%5C%5Cb%20%5C%5Cc%20%5Cend%7Bbmatrix%7D) : {: Z9 E. K1 v& M8 J! K
: {: Z9 E. K1 v& M8 J! K
可結出
- h$ p; \' P1 |+ T) T%20%26-(%CE%BBY_%7BB12%7D%2BY_%7BA12%7D)%20%5C%5C%20-(%CE%BBZ_%7BB12%7D%20%2BZ_%7BA12%7D%20)%26%200%20%26%20(%CE%BBX_%7BB12%7D%2BX_%7BA12%7D)%5C%5C%20(%CE%BBY_%7BB13%7D%2BY_%7BA13%7D%20)%26(%CE%BBX_%7BB13%20%7D%2BX_%7BA13%7D)%260%5Cend%7Bbmatrix%7D%20%5E%7B-1%20%7D%5Cbegin%7Bbmatrix%7D%20X_%7BA12%7D%20-%CE%BBX_%7BB12%7D%20%5C%5C%20Y_%7BA12%7D%20-%20%CE%BBY_%7BB12%7D%20%5C%5C%20Z_%7BA13%7D%20-%20%CE%BB%20Z_%7BB13%7D%20%5Cend%7Bbmatrix%7D) * V- i1 C, P$ t5 P( k3 \
* V- i1 C, P$ t5 P( k3 \
把a、b、c帶入(2)式可到旋轉矩陣R,把任意一點坐標帶入(1)式可得Δ。
. g2 t$ }" k' [7 _/ c% q8 w: i9 P. k5 ?( E* g6 m2 D5 I" M* e( m
9 E4 d1 L! a v1 ?9 k4 f8 Q
- K& w# ?/ Q" c( Q; z! Z作者:梁間5 D6 N. i; m2 V! e$ h2 O4 \
鏈接:https://www.jianshu.com/p/58cf5655f9a9! ~. \5 o& a5 L9 ^1 e; ^. k
來源:簡書
; h7 w9 \. I; L. K& F著作權歸作者所有。商業轉載請聯系作者獲得授權,非商業轉載請注明出處。
) \9 k1 H# c2 D: O) V+ b/ I3 b o8 t; m# M: l" ]/ h6 {3 h
作者: 水水5 時間: 2025-7-29 19:23
方法二,這里提到了SVD算法
! h: ^' V5 Q3 q% V7 {& w+ k9 }
通過實際的坐標點例子,來直觀解釋通過SVD求對應的坐標系關系。
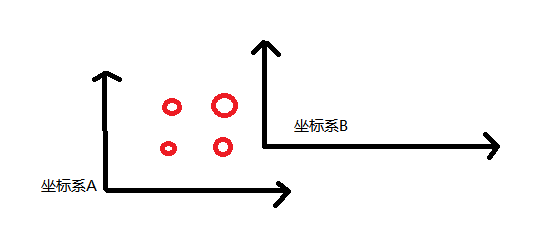
已知四個點在坐標系A中的坐標為:
(0, 0, 0); (1,0,0); (1,1,0); (0,1,0)
可得矩陣A為
, Y* ?6 z$ P _2 z- E; ?) V' P
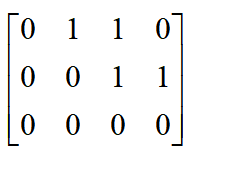
, W) i B U1 r8 d$ D矩陣A這四個點在坐標系B中的坐標為:
(2,2, 2); (3,2,2); (3,3,2); (2,3,2)
可得矩陣B為
9 a. l l- `- y& U3 n& c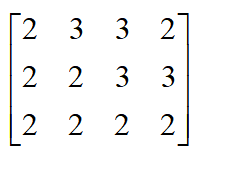 ( Q1 m e6 U( q+ O& p' D1 F
( Q1 m e6 U( q+ O& p' D1 F
矩陣B步驟一:求兩個數據集的質心
根據上述公式,可得質心為
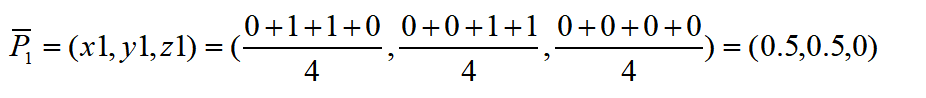

步驟二:將兩個數據集的質心移動至同一個點,即只存在于一個旋轉的轉換關系。
對應坐標系中的點同時減去質心,計算后的矩陣A和B分別為
b$ o# i- X) y5 O& t0 c6 a

) ~: N) k2 c) k計算后的矩陣A& J. d4 X" \/ F [
 ( y, e C% }% A
( y, e C% }% A
計算后的矩陣B備注:此處的矩陣A和矩陣B一樣,因為舉得例子較為特殊,只存在平移關系。計算過程通用。
步驟三:通過SVD算法計算旋轉和平移關系。
定義一個3X3的矩陣,將矩陣A的每一行數據與矩陣B進行點乘,會產生四組3X3的矩陣,將這四組數據求和,得到最終的3X3的矩陣,就是我們需要用SVD算法來進行奇異值分解的矩陣H。
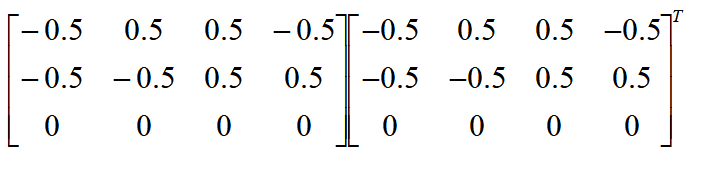
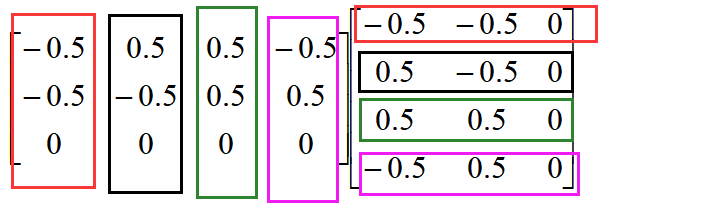
上述公式中,顏色相同的框內數據進行點乘,構成3X3的矩陣a1,a2,a3,a4。
矩陣H = a1 + a2 + a3 + a4。計算結果如下
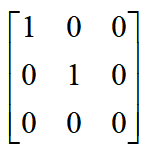
通過SVD算法分解該矩陣,這里直接通過MATLAB接口調用,具體原理在前面的章節中已描述。
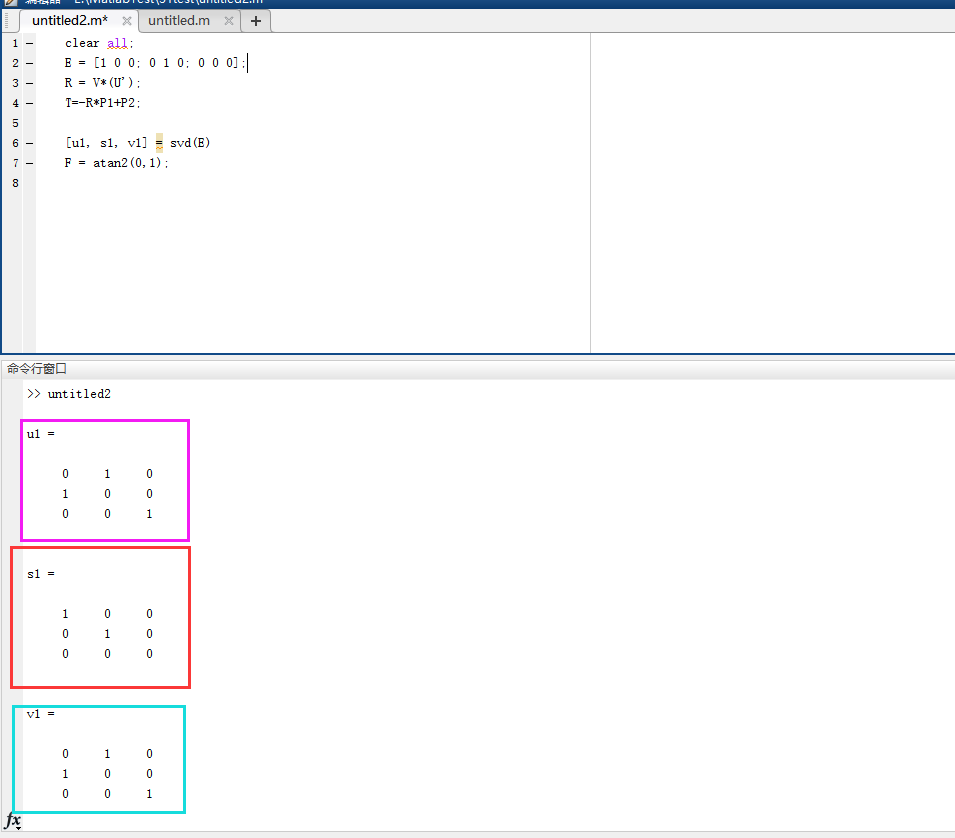
步驟四:計算旋轉和平移關系
根據上述求出的u1和v1,可求得旋轉矩陣R為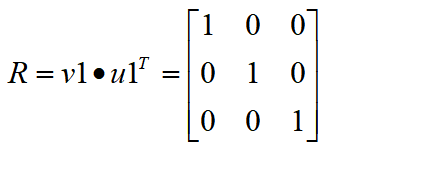 將該旋轉矩陣轉為歐拉角則Rx = 0, Ry = 0, Rz = 0。
將該旋轉矩陣轉為歐拉角則Rx = 0, Ry = 0, Rz = 0。根據公式
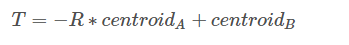 得平移矩陣為
得平移矩陣為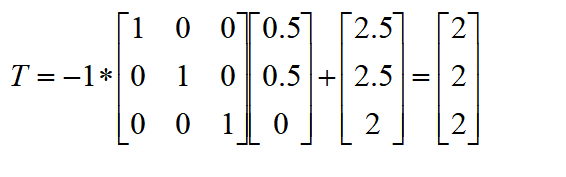
總結:如果在實際項目中,需要獲取多臺設備間的關系,如機器人相對于產品間的關系,或者機床相對于產品的關系,則該方法較為實用。注意:在實際的選擇參考點時,不要在一條線上選點。如上述選的四個點,要求不能共線。要不然會減少有效數據。
& p- W$ k, s1 Q, \2 D0 L
作者: DaedraMech 時間: 2025-7-29 20:37
本帖最后由 DaedraMech 于 2025-7-29 20:42 編輯
( I! R- v% J9 T% A7 |& Z6 U8 L/ h9 n# N+ W' r* d; e
沒想到水水大俠對此問題如此孜孜以求,鉆研精神和信息獲取能力令小弟佩服,我比較功利,方法能解決問題就行。$ }* c5 U. ^2 A- \
* n2 U4 M5 d) ~, ?! x0 G* C% }
我把之前回復中的齊次變換矩陣改一下符號,樓主可以對比下和文章中的表達方式是不是一回事:
/ @' H1 X l% U1 B6 }- e[attach]577263[/attach]
V* T3 W9 f. [( J6 N: i[attach]577264[/attach]
1 M* X$ C- k4 }# A3 t1 p平移、旋轉、縮放這類坐標變換我們統稱為線性變換。平移和縮放非常簡單,沒什么好說的,重點就是如何求得旋轉矩陣R,上述兩種方法就是通過純代數的方法求解R。
5 t% X* G( f& n5 w$ f7 y2 E你用什么方法和選擇的工具有關,上述兩種方法多用在圖像處理和機器學習中,算法工程師手里的工具是集成編程環境,是代碼,采用代數方法自然是比較直接的。但要知道矩陣可是聯系代數和幾何的橋梁啊,而我們則掌握了強大的幾何工具SW,利用【旋轉矩陣可以表示坐標系】這一幾何意義我們可以直接得到R,完全不需要上面繁瑣的運算。
4 r& R! d0 h; X I: k: m8 A
作者: 水水5 時間: 2025-8-3 20:15
本帖最后由 水水5 于 2025-8-3 20:21 編輯 $ g- v5 V1 Y2 Z
DaedraMech 發表于 2025-7-29 20:37+ V8 h4 X, ?; C j+ [/ d# x
沒想到水水大俠對此問題如此孜孜以求,鉆研精神和信息獲取能力令小弟佩服,我比較功利,方法能解決問題就行 ...
, z- p" ~; |$ T& Q感謝大俠的持續教誨。大俠如果有,從變換矩陣導出歐拉角,的計算公式,恭請再給明示下。; r+ i; G2 }* e0 S& l9 R# s- T
$ `6 P# ~! u% j4 A/ k2 j
經過又一個周末的摸索和學習,我已經學到了旋轉矩陣的測量方法,并且通過計算一個點的坐標在兩個坐標系中的坐標值進行了驗證。' [# V) `4 G& o# p& b( u
! x# V6 i( c: v4 z這是第一步,下一步是求歐拉角。
% B3 h: O% z: O& }! r) x) u2 ~! [$ D6 V/ \3 x6 b) c
我最終的目的是: Z, f/ _' x) b
“在機器人示教工具坐標系的時候,不需要再繁瑣的用6點法搞一個小時示教,而是我作為機械工程師,可以直接從三維中計算出,通過計算,直接可以提供XYZABC的數值”( K" w9 n6 ^ ~% a/ D' z; J
6 O5 H$ t% n* I" T! k5 F但是這里面有個難題,我不知道機器人工具坐標系參數他是采用的哪種形式的歐拉角
0 v3 H) n9 P3 B下圖是我的作業1 G5 u, i1 N- G9 o" T$ ^! W$ y ?
[attach]577369[/attach]
+ ~' Z) ~# X5 ?4 ]% @% y# Q
作者: DaedraMech 時間: 2025-8-6 20:03
本帖最后由 DaedraMech 于 2025-8-6 20:06 編輯
: z! o0 z# A% T, ^( k( I) W. }6 j; ^' A* P
歐拉角其實也不難求出,就是麻煩點。
# \: h- a/ z6 ]3 b
8 H/ t" j7 `8 D2 \4 C假設你手上的示教器里面歐拉角就是按照常規的Roll-Pitch-Yaw順序(ZYX順序)定義的,那我們不妨把單獨繞Z、Y、X軸的旋轉矩陣從左到右依次乘起來,看看最終的旋轉矩陣里各個元素的表達式都是啥。
+ q" w8 ^0 H) D' `. H* B: s[attach]577485[/attach]
" ~, n5 r; z6 ~" ?6 P1 y! q# z從上面的結果可以看出,通過對矩陣中特定元素之間的運算,我們是能夠分離出繞特定坐標軸的轉角的,即:
Z# ^$ ^4 f& d4 d H[attach]577489[/attach]
5 i- c0 H- w6 v如果不知道示教器中歐拉角是如何定義的(并且上述順序錯誤的話),就需要再交換單軸旋轉矩陣的乘法順序,獲得新的表達式再次實驗。(也可以直接在示教器上輸入角度看機械臂到底先繞哪個軸旋轉)( T) ?: Z9 W' l# q
/ F& `- B/ s+ v+ G- U& z
另外可以想象到,空間中一定存在某個軸,能夠讓坐標系一步到位,直接一次旋轉到最終位置,而這就要用到四元數。所以如果示教器還支持四元數輸入的話,也可以將旋轉矩陣轉化為四元數:
2 e+ [/ h8 ]5 D" g0 e[attach]577490[/attach]* E3 V" v7 ?; R/ {' K
四元數中xyz表示了轉軸的方向,w表示了繞這個軸的轉角,其值為轉角的半角余弦值。
( J1 i% M% F4 a0 ~! [6 w" B* Y# Y8 b) b$ K. k
[attach]577491[/attach]/ y( a5 J+ k5 d1 J: s6 t) e* k1 K
作者: 水水5 時間: 2025-8-9 08:15
本帖最后由 水水5 于 2025-8-9 08:23 編輯
& @8 ^6 S2 |0 n) u6 Q; dDaedraMech 發表于 2025-8-6 20:03
/ V: z! k- [. G& l1 L歐拉角其實也不難求出,就是麻煩點。7 r& @9 a4 o5 w
2 o; \+ O( _! a/ l4 R
假設你手上的示教器里面歐拉角就是按照常規的Roll-Pitch-Yaw順序(ZY ...
0 I6 v. @* A9 l: f% N感謝大俠的熱情回復。匯報下進展:
) \) |; b9 j/ j) c% \4 K* v
: ^& k" @8 M5 \4 b首先證明了旋轉矩陣是對的,第一步已經完成,
6 M! v7 u% K% e第二步,我找了那些計算歐拉角和四元數的公式,公式應該是沒錯的。雖然歐拉角的解不唯一,但是四元數是唯一解。經過比對,還是和示教器中的數值有一定的差距。8 D! o0 u5 b% R3 H4 o8 {
[attach]577592[/attach]
8 i# f: J) C# R經過分析,機械安裝有一定的誤差,手爪又這么長。所以至少證明了理論計算是正確的。但是實際應用,還是要修正。免不了還是要示教一下。
9 Q9 w: p' V5 j* }; `- y% p7 O第三步,通過咨詢得到 歐拉角的旋轉方式。還未進一步計算,等下次有機會了再實驗。7 t: S: R( C" g0 g+ U6 v
[attach]577593[/attach]' `: b1 A7 B2 X, ]
這是FANUC對坐標系歐拉角的描述,市面上絕大多數機器人,都是遵循固定坐標系XYZ這樣的一個旋轉順序。& Z0 [8 p7 _# Q2 f
o& j! J G# t0 ~- J! l8 {上士聞道,勤而行之;中士聞道;若存若亡;下士聞道,大笑之。不笑不足以為道。
' n" G9 G4 ?4 B感謝各位的技術支持,感謝論壇。4 ^, z9 J* L+ D% o9 @$ b* T
作者: 水水5 時間: 2025-8-9 08:38
DaedraMech 發表于 2025-8-6 20:038 c. t( P: _! ~$ U0 H6 [
歐拉角其實也不難求出,就是麻煩點。 @0 r7 m9 H1 Q+ ~
# q. Q( \: F7 B
假設你手上的示教器里面歐拉角就是按照常規的Roll-Pitch-Yaw順序(ZY ...
& ^* X! \2 O9 y3 Z0 l大俠有沒有 mathcad 教程 源文件?9 J; j( ]" n: a" {
" U O7 T$ @7 ^0 @9 t0 e" H
您給出的公式的求解,還是有點一知半解。數學沒學好,尷尬
8 \& M1 K6 d! ^2 s: }
作者: ckc521 時間: 2025-8-12 22:39
歐拉角旋轉很簡單的,不管是什么順規的旋轉,都可以用基本旋轉矩陣推導出來,但是歐拉角的萬向鎖問題很煩人,雖然有算法可以解決.
| 歡迎光臨 機械社區 (http://m.whclglass.com.cn/) |
Powered by Discuz! X3.5 |


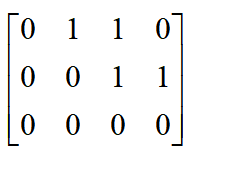
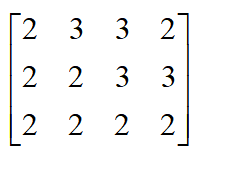 ( Q1 m e6 U( q+ O& p' D1 F
( Q1 m e6 U( q+ O& p' D1 F
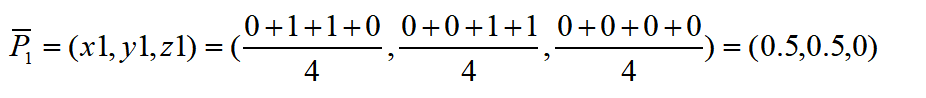


 ( y, e C% }% A
( y, e C% }% A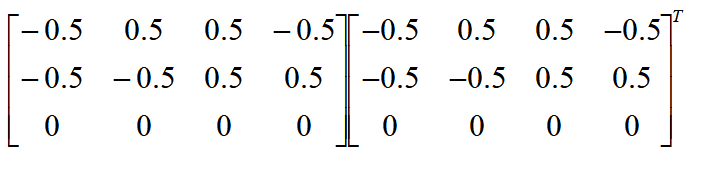

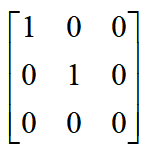

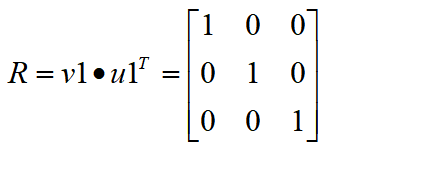 將該旋轉矩陣轉為歐拉角則Rx = 0, Ry = 0, Rz = 0。
將該旋轉矩陣轉為歐拉角則Rx = 0, Ry = 0, Rz = 0。