機械社區
標題: 清華將線性代數教材改為英文版,學生稱更通俗易懂;熬夜變傻有了科學依據 [打印本頁]
作者: Insigne 時間: 2019-11-4 10:37
標題: 清華將線性代數教材改為英文版,學生稱更通俗易懂;熬夜變傻有了科學依據
1.NASA將直播波音Starliner太空飛船的關鍵測試
0 X1 Q. ~5 e( j8 E
4 E4 F6 ?" _3 K1 a0 e1 L9 \
- h7 V* e7 p% P6 C4 ]) V" V$ n
據外媒CNET報道,隨著美國宇航局(NASA)進一步推動將近十年來首次載人航天發射帶回美國本土,波音公司新的Starliner航天器的測試將意味著一次大考驗。
: V7 q- C7 D0 b& M; J1 A: _
目前,該Starliner航天器已經出現在新墨西哥州的白沙導彈試驗場的測試臺上,等待定于太平洋時間周一上午6點進行的逃生系統測試。該測試的目的是確保在發射臺上的緊急情況下,四臺中止發動機和控制推進器能夠點火,從而將太空艙和宇航員帶離潛在危險。
Starliner是美國宇航局(NASA)已簽約的兩架新型航天器之一,這是其商業載人航天計劃的一部分,該航天器開始將宇航員飛往國際空間站。另一個是SpaceX 載人龍飛船 ; 這兩艘飛船在開發和測試過程中都面臨著延誤,這促使美國宇航局局長吉姆·布里登斯廷公開向這些公司施加壓力。
2 f" D5 w" |4 Y4 ?3 x
2.清華將線性代數教材改為英文版,學生稱更通俗易懂
, r1 h1 A, F2 N; n/ F" b" g% B7 o' _4 ?

5 M4 G' S6 s3 F0 s) O2 a. e% K
近日“清華大學將線性代數教材改為英文教材”話題引熱議。剛剛參加完該課程期中考試的清華大學大一新生在接受媒體采訪時表示,適應了這本教材的體系之后,從內容上來說,這本教材更通俗易懂,容易理解。
) K l/ S( U$ D N
據介紹,教材的正式更換將于2019年新生入學,此前學校采用的都是中文版教材。對于語言問題,有學生接受采訪時表示,剛開始用的時候肯定會有語言上的障礙,但是從語言上來講,經常閱讀教材,適應了它的體系之后,其實還可以。
. o @! M! ^' @" k1 F
3.德國力推新能源汽車發展,2030年前將建100萬個充電樁2 F& P' |( Z0 p- k+ J' I
, [; l( ~% P. X: `

) y6 g" ]4 l: F) w" a& }
德國總理默克爾3日表示,德聯邦政府將攜手汽車業界推動出行方式的轉型。為此,她即將在同汽車業界的對話中探討新能源汽車購買補貼、充電設施建設和汽車業轉型對就業的影響等議題。默克爾表示,德國政府希望最晚到2030年能在該國建成100萬個充電樁。
作為傳統汽車大國,德國在全球電動車蓬勃發展的大趨勢下轉型步伐顯得滯后。德媒指出,德國政府此前設定的2020年左右電動車總量達到一百萬輛的目標一再跳票,而應對氣候變化的緊迫性亦給德國汽車業帶來壓力。
! t7 W, x# W" H) `) [- o
4.羅永浩上了“老賴”名單
4 P4 g/ C" m+ [ a q% z3 @4 O5 L" j' |

5 f* p% l) a& W; Y" A
11月3日下午消息,北京錘子數碼科技有限公司及羅永浩被法院限制消費。
2 g5 k8 E: Z! O6 l$ G5 {" Z) B
“彪悍的人生不需要解釋。”這句話或能成為羅永浩的一個注解。從新東方英語老師,到砸西門子冰箱、質疑方舟子而名聲鵲起,成為輿論領袖,創業前的羅永浩可謂順風順水。但自2012年宣布創業做手機以來,羅永浩接連遇到挫折,發布的幾款手機叫好不叫座。今年再次創業的羅永浩看準了電子煙的風口,不想近期遭遇最嚴監管政策。
# T6 o7 H+ {* @& p! t( Q* U
11月3日晚間,羅永浩通過微博回應稱,已還3億公司債務;會繼續努力,在未來一段時期把債務全部還完,哪怕以“賣藝”之類的方式。
7 l# J1 g: ?+ A5 X/ y. p
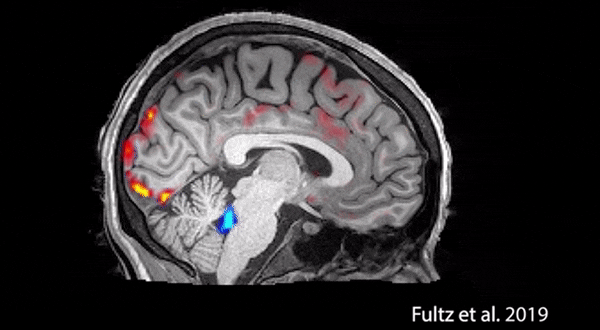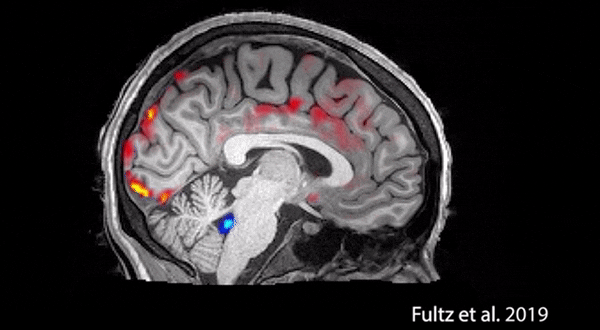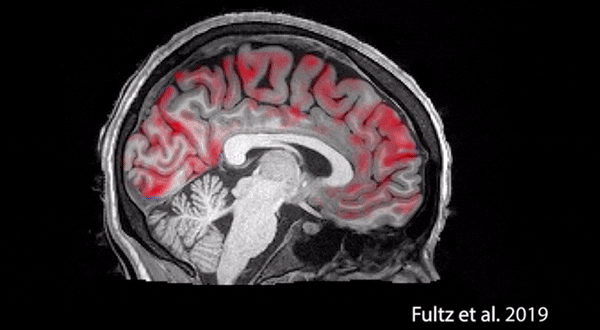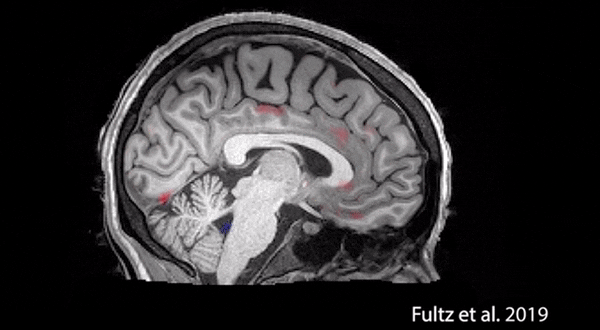
5.熬夜變傻有科學依據:科學家稱睡眠時間大腦會開啟“自動清洗”
' ]) m6 e$ l( P3 G5 b( }9 p2 B4 K& {/ m9 h
! f1 H. Y; P: Y4 _
據據外媒報道,,波士頓大學的科學家們通過實驗證實了睡眠的“清洗”作用。
. i! [! s. ?6 _6 i# S% A# Q- X5 H
據悉,科學家們拍下了大腦自身清洗的過程,其中紅色是血液,藍色是腦脊液。血液會周期性地大量流出大腦,腦脊液趁機涌入,清除毒素。科學家表示,睡眠期間,神經元會同步活動,使大腦的血氧濃度出現周期變化。而醒著的時候,神經元不會同開同關,也就導致無法讓大腦血量下降到足夠低的水平。因此這樣的清洗,只有睡著后才能做到,否則腦脊液沒法趁虛而入。被清除的毒素包括β-淀粉樣蛋白,而這正是導致阿爾茨海默氏癥的一大元兇。
) S& i5 D: S5 l. P. k+ {
鎂客網
. s+ p/ W8 T7 l8 N
! r0 q, S: U# x- ?
作者: 魍者歸來 時間: 2019-11-4 10:52
拋開語言障礙的話,確實外文的教材更好懂一些,我現在學專業課都是日文版和漢譯版對照著看,比看某些XX規劃教材要更好一些
作者: Q807859983 時間: 2019-11-4 11:08
確實外文的教材更好懂一些,
作者: 遠祥 時間: 2019-11-4 21:26
所以說同學們都愛讀白話文。。。
作者: jackgong 時間: 2019-11-7 23:21
website:math.mit.edu/~gs/linearalgebra/
9 T! j- C8 O4 vTable of Contents for Introduction to Linear Algebra (5th edition 2016)+ }1 ]" u* c2 G. K5 `8 X
1 Introduction to Vectors4 X0 a* j$ N0 a' u
1.1 Vectors and Linear Combinations
& o1 T7 u2 o C/ z! L1.2 Lengths and Dot Products
1 L0 \- E% W, _' k8 N0 l$ o0 g1.3 Matrices
. y" j2 t* |/ W6 R5 B) @% c- _2 Solving Linear Equations( J% V+ S, U2 f0 V9 I
2.1 Vectors and Linear Equations8 I2 O' J; e7 I- n& y! ^2 N
2.2 The Idea of Elimination! D6 }" c7 ]1 n% g ^
2.3 Elimination Using Matrices
! ~- x( Q9 t- q% W7 Q# R" r" R2.4 Rules for Matrix Operations
) G4 b% [& m- { n2.5 Inverse Matrices
4 m v$ _- V2 M2 f/ k2.6 Elimination = Factorization: A = LU5 [/ E+ T& \7 J# Z# u) {, c5 F
2.7 Transposes and Permutations" ~2 H0 ]) A; p
3 Vector Spaces and Subspaces
" m: i/ [5 D# v6 v$ n/ U3.1 Spaces of Vectors) n( K: [+ Y6 P1 ]& T2 f' C
3.2 The Nullspace of A: Solving Ax = 0 and Rx = 0
" X0 q" c9 F. X* i3.3 The Complete Solution to Ax = b" s& D; E+ ]: I+ q# _& ^8 g
3.4 Independence, Basis and Dimension& J/ `1 ], `$ \. g" Z- {
3.5 Dimensions of the Four Subspaces4 u0 `+ B9 z$ M; j
4 Orthogonality! g7 u9 T; f2 D3 h8 O% }3 E
4.1 Orthogonality of the Four Subspaces; o4 a4 j+ e# ?$ g" C3 ?. p- \
4.2 Projections
. t3 A4 C5 T( j0 Z% f, p4.3 Least Squares Approximations$ W0 D4 [9 X: [; y0 t
4.4 Orthonormal Bases and Gram-Schmidt
* b' D1 {. S4 c- |+ u' M5 Determinants5 F" l( c$ _8 \1 \1 r" m* X4 `
5.1 The Properties of Determinants+ M- d! B! y g& J: o8 Z) |+ l5 J
5.2 Permutations and Cofactors
( D3 z1 m: m" H8 h5.3 Cramer’s Rule, Inverses, and Volumes, B# o& \" d0 c
6 Eigenvalues and Eigenvectors
3 T3 z1 o2 V3 f1 R( }0 A4 |6.1 Introduction to Eigenvalues
# \# O; g9 |0 Q9 y J6.2 Diagonalizing a Matrix: M9 ^6 _4 g' T* X
6.3 Systems of Differential Equations
6 y0 [. e# e% Y8 Y q, Q4 s6.4 Symmetric Matrices; ]3 l/ _, @- a" L* a1 H
6.5 Positive Definite Matrices7 b; r% Z( u Y9 k
7 The Singular Value Decomposition (SVD)
7 c0 {; `. @) j3 r* E4 r9 e5 q7.1 Image Processing by Linear Algebra
& e' b* c, `. I& l T7.2 Bases and Matrices in the SVD
A8 O/ u( F$ c7.3 Principal Component Analysis (PCA by the SVD)6 }7 t Z o/ K5 T% n' c I# n- T
7.4 The Geometry of the SVD
+ n* b1 O+ l2 U5 |, i, k8 Linear Transformations4 M; m4 p7 z( B* p0 k) w
8.1 The Idea of a Linear Transformation
8 d/ o5 o& b; y$ V- s8.2 The Matrix of a Linear Transformation& n% f; a4 _) O; V2 S* j- D
8.3 The Search for a Good Basis3 q$ p9 f- f. f) J
9 Complex Vectors and Matrices
: O# b& I3 g& Q9 _' U! c: ~% ~% K9.1 Complex Numbers. P+ b! W3 `2 s2 @) w
9.2 Hermitian and Unitary Matrices& a8 R6 n. U. q( @2 p
9.3 The Fast Fourier Transform
# o+ i. `6 k/ T* r10 Applications
4 f: I J0 F' W! I( L/ j10.1 Graphs and Networks: _% I: b( w3 N" D
10.2 Matrices in Engineering/ e4 ]9 {) L$ Z( u& J
10.3 Markov Matrices, Population, and Economics
! M' M& a& R- z10.4 Linear Programming
}# i% M" c8 ]/ Y$ w, {4 u: C10.5 Fourier Series: Linear Algebra for Functions9 N8 w# I7 |0 h: ^: A) Z3 [9 k
10.6 Computer Graphics
/ h; P' c) e1 A- z10.7 Linear Algebra for Cryptography, Q+ A$ V+ Z( Y5 S$ K
11 Numerical Linear Algebra
9 l( h1 b, F4 _+ L3 }11.1 Gaussian Elimination in Practice
" N9 I* C/ \: }& I11.2 Norms and Condition Numbers. a# n+ w. s1 j* ^2 D( V% o
11.3 Iterative Methods and Preconditioners# i5 J- W) q; ^+ \
12 Linear Algebra in Probability & Statistics
& A8 `0 t* X" c) W5 B12.1 Mean, Variance, and Probability
9 f+ g+ k. F8 F$ O6 x12.2 Covariance Matrices and Joint Probabilities
4 Q0 Z1 h% w. D) O3 e; m12.3 Multivariate Gaussian andWeighted Least Squares- s: P7 F3 M& j
Matrix Factorizations
% Q; n* P& Q5 ~' W6 O1 W! eIndex+ S8 h! u% O* E$ `
Six Great Theorems / Linear Algebra in a Nutshell; f( G7 d$ M& n U3 u- H" |3 `% H
| 歡迎光臨 機械社區 (http://m.whclglass.com.cn/) |
Powered by Discuz! X3.5 |





